-
Recent Posts
Archives
Categories
Meta
Math Worth Reading
Ode to the Infinite
From time to time, I participate in the weekly Indie Ink writing challenge. I had not yet published a response on this website, as my previous challenges did not lend themselves to the general theme that I have in my head for what belongs here. However, this week I found inspiration in our system of numbers. The result is a response to the prompt “This is what it’s like..,” which was given to me by Lazidaisical. I, in turn, asked Barb Black to write about the quadratic formula (I’ve been preparing lectures for summer algebra and, apparently, have numbers on the brain).
In many ways, this is also a response to the questions that I get from my algebra students. After spending a good deal of the course building toward it, we introduce the quadratic formula. One of the difficulties of the formula is that the solutions it produces often involve the square roots of negative numbers. This confuses many students, as they have been told for years that negative numbers don’t have square roots. This is made even more difficult by the unfortunate fact that these square roots are referred to as “imaginary” numbers.
Happy Tau Day 2011!
Today is Tau Day. I’ve mentioned the constant τ previously, so I won’t go into it again. Instead, enjoy the following musical composition, based upon the decimal digits of τ.
Struggling with Hard Problems
Yesterday, I came across an interesting post by Allison at Infinigons. She reminds us that we must remain fearless in the face of difficult problems, and attempt to do something, rather than give problems a cursory once-over, then run to Google. It is worth reading her post for the details.
The example she gives is a fun problem, which I would be happy to discuss with any of my three or four readers, should they wish to comment below. The answer that I got was \(\frac{4\sqrt{2}}{3}-\frac{5}{3}\approx 0.219\), if you want to check your (or my) work (I’m pretty confident of that solution).
That being said, I think that the emphasis of the linked post should really be placed upon the willingness to think about and work with hard problems, in mathematics and beyond, without instantly looking for an authority to answer the problem.
Posted in Education
Tagged education, games, problem solving
Comments Off on Struggling with Hard Problems
Dimensions
A couple of weeks ago, I ended up trying to explain my current line of research to one of my wife’s friends. It turns out that it is not that simple to describe. To begin consider this deceptively simple little question: what is a three dimensional figure?
Most people can probably give examples of three dimensional figures based on experience in elementary or secondary lessons in geometry. When pressed, I imagine that many could also give some kind of description of a three dimensional figure. For instance, we might state that a one dimensional object has only length, while a two dimensional object has length and width, and a three dimensional object has length, width, and height.

Hence we might define dimensions as follows:
The dimension of an object is the number of directions required in order to measure it.
There is a nice intuition here, and there are some interesting relationships between objects of different dimensions under this interpretation, but there are also some problems.
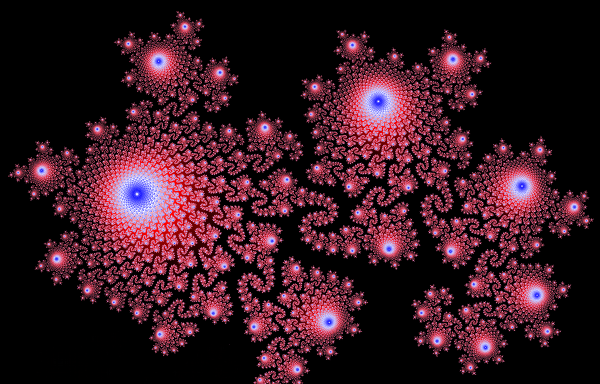
Spring Flowers on Indie Ink
“Spring Flowers,” one of my images of the Mandelbrot set has been selected for publication on the site Indie Ink. Indie Ink is a nifty website that encourages people to produce words and images in an environment that fosters creativity without pressure.
For any Indie Inkers that are stumbling across this website for the first time, the image on Indie Ink was created using a lot of math and a little bit of computer horsepower. I have written at some length about the Mandelbrot set in the past and, if you are interested, I would encourage you to have a look.