A large portion of the “standard” precalculus curriculum consists of a rather tedious recitation of trigonometric identities. I am largely of the opinion that there are only a couple that one really needs to know—for example, the Pythagorean identity (\(\sin(\theta)^2 + \cos(\theta)^2 = 1\) for all \(\theta\)), one of the angle addition formulæ (e.g. \(\cos(\theta+\varphi) = \cos(\theta)\cos(\varphi) – \sin(\theta)\sin(\varphi)\) for all \(\theta,\varphi\)), and the law of cosines (essentially the Pythagorean theorem with a correction term) immediately come to mind as important results. In the last quarter, while teaching precalculus class, I was introduced to a couple of proofs that I had not seen before. I don’t get the impression that either proof is that unusual or original, but I do think that they are both rather slick. I’m putting them up here for future reference.
Angle Addition Formulæ
Theorem: Given any two angles \(\alpha, \beta\), we have the identities \[\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) – \sin(\alpha)\sin(\beta) \quad\text{and}\quad \sin(\alpha + \beta) = \cos(\alpha)\sin(\beta) + \sin(\alpha)\cos(\beta).\]
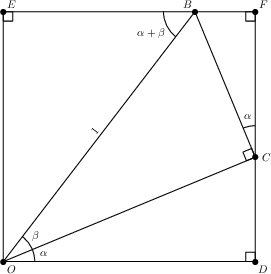
Proof: It is possible to obtain angle addition formulæ for both sines and cosines with one picture. The argument is as follows: first, we need to angles to add together, say \(\alpha\) and \(\beta\). We are going to draw them so that \(\alpha\), \(\beta\), and \(\alpha+\beta\) all live in quadrant I, though the argument can be generalized to other quadrants without too much additional work (exercise: do this).
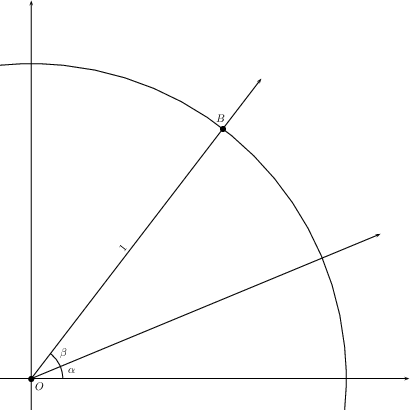
Note that the point \(B\) is the point on the unit circle where the ray emanating from the origin with angle \(\alpha+\beta\) intersects, hence \[B = (\cos(\alpha+\beta),\sin(\alpha+\beta));\] we’ll come back to this later. Next, we can construct a line through \(B\) that is perpendicular to the ray emanating from the origin with angle \(\alpha\)—call the intersection \(C\).
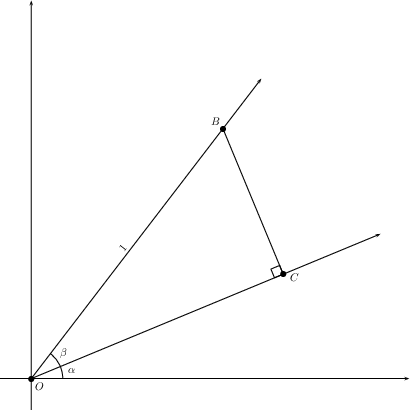
Similarly, construct a segment perpendicular to the \(x\)-axis through \(C\), and a segment perpendicular to the \(y\)-axis through \(B\)—these are the points \(D\) and \(E\), respectively.
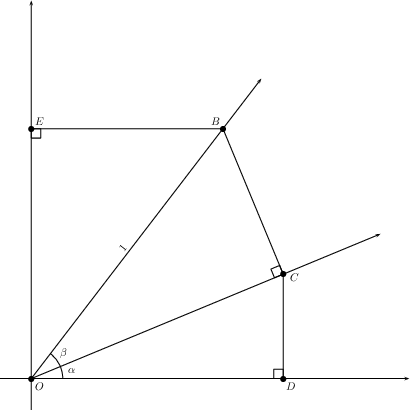
We finish the figure by extending the segments \(EB\) and \(DC\) until they intersect at a point \(F\). Note that we now have a rectangle \(ODFE\).
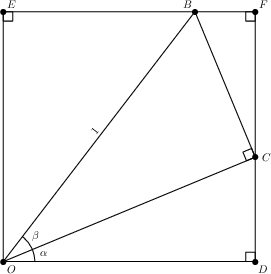
The line \(OB\) is transverse to the parallel lines \(EF\) and \(OD\) (since these are opposite sides of a rectangle), thus \(m\angle EBO = m\angle COD = \alpha+\beta\). Moreover, since \[m\angle FCB + m\angle BCO + m\angle OCD = \pi,\] it follows that \(m\angle FCB = \alpha\). These are labeled in the next figure.
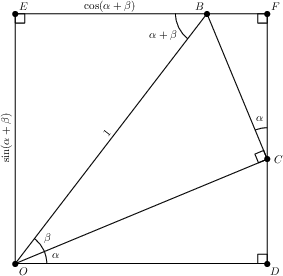
Recall that \(B = (\cos(\alpha+\beta),\sin(\alpha+\beta))\). This gives us the lengths of the segments \(OE\) and \(EB\).
Via some right triangle trig identities on \(\triangle OCB\) (in particular, the identities given by the mnemonic “SOH CAH TOA”), we have that \(OC = \cos(\beta)\) and \(BC = \sin(\beta)\).
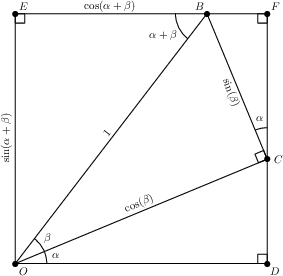
Using the same trig identities, this time applied to \(\triangle ODC\), we have that \(OD = \cos(\alpha)\sin(\beta)\), and \(CD = \sin(\alpha)\cos(\beta)\).
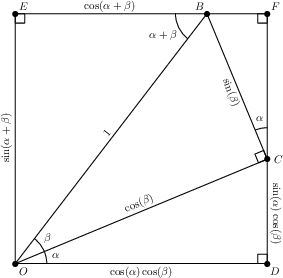
Finally, repeating the same argument on \(\triangle BFC\), we have \(BF = \sin(\alpha)\sin(\beta)\) and \(CF = \cos(\alpha)\sin(\beta)\).
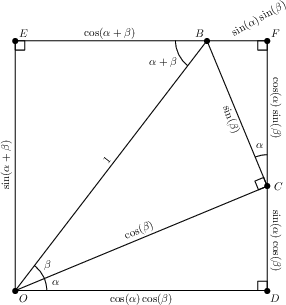
But this figure essentially completes the proof. Since opposite sides of a rectangle have the same length, the vertical sides give us \[\sin(\alpha+\beta) = \cos(\alpha)\sin(\beta) + \sin(\alpha)\cos(\beta),\] and the horizontal sides render \[\cos(\alpha+\beta) + \sin(\alpha)\sin(\beta) = \cos(\alpha)\cos(\beta).\] Note that, after moving the \(\sin(\alpha)\sin(\beta)\) term of the second identity to the right-hand side, these are the proposed angle addition formulæ.
Law of Cosines
Theorem: Suppose that an arbitrary triangle has sides of length \(a\), \(b\), and \(c\), with the angle \(\theta\) opposite the side \(c\). Then \[c^2 = a^2 + b^2 – 2ab\cos(\theta).\] Note that if \(\theta\) is a right angle, then \(c\) is the hypotenuse of a right triangle and \(\cos(\theta) = 0\), giving the Pythagorean Theorem. Hence we may regard the Law of Cosines as a generalization of the Pythagorean Theorem with some kind of correction term.
Proof: We may assume that the triangle is oriented such that \(\theta\) is at the origin and one of the two “legs” is along the \(x\)-axis in the Cartesian plane. Labeling the vertices such that vertex \(A\) is opposite the side with length \(a\), \(B\) is opposite \(b\), and \(C\) is opposite \(c\), we obtain the figure shown below.
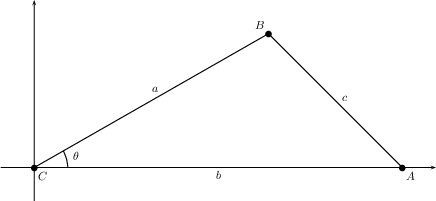
Since the point \(A\) is along the \(x\)-axis, the \(y\)-coordinate of \(A\) is zero, and since the distance from \(A\) to the origin (\(C\)) is the length of the corresponding leg of the triangle, we have that the \(x\)-coordinate of \(A\) is \(b\). That is,\[A = (b,0).\] To determine the coordinates of \(B\), note that the ray from \(C\) through \(B\) must intersect the unit circle at some point \(B’\), as shown below.
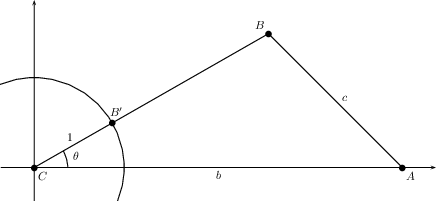
From the definitions of sine and cosine on the unit circle, we know that the coordinates of \(B’\) are given by \(B’ = (\cos(\theta),\sin(\theta))\). Then, as \(\triangle ABC\) is similar to \(\triangle AB’C\), it follows that \[B = (a\cos(\theta),a\sin(\theta)).\]
On the one hand, we know that \(d(A,B) = c\) (that is, the distance from \(A\) to \(B\) is \(c\) units). On the other hand, the distance formula tells us that \[d(A,B) = \sqrt{(a\cos(\theta)-b)^2 + (a\sin(\theta))^2} = \sqrt{a^2(\cos(\theta)^2 + \sin(\theta)^2) – 2ab\cos(\theta) + b^2}.\] Applying the Pythagorean Identity \(\cos(\theta)^2 + \sin(\theta)^2 = 1\) and squaring, we obtain \[c^2 = d(A,B)^2 = a^2 – 2ab\cos(\theta) + b^2,\] which is the desired result.
