In the past, we have spent a significant amount of time discussing the Mandelbrot set and variations thereon. We saw that each Mandelbrot, multibrot, and Julia set can be characterized as a set of complex numbers that behave “nicely” with respect to a function of the form \(f(z) = z^e + K\), where the choice of \(K\) gives us either a multibrot or Julia fractal. These functions are only a very small subset of all possible complex valued functions, and there are many interesting fractals that can be rendered by examining the behaviour of other kinds of functions. In this post, we will examine a function with a relationship to an open problem in number theory called the Collatz conjecture.
The Collatz Conjecture
Choose a positive integer. If the integer is even, then divide it by 2, otherwise, multiply it by 3 and add 1. Take the result, and perform the same process again, and again, and again. The German mathematician Lothar Collatz posited that, regardless of the initial choice, this procedure would produce a sequence that eventually reaches 1.
For example, suppose that we start with 10. 10 is even, so we divide by 2 to get 5. As 5 is odd, we multiply by 3 and add 1, which gives us 16. 16 is even, so the next number in the sequence is 8, followed by 4, 2, and 1. For most numbers less than 100, it is fairly easy to perform this procedure by hand and confirm that the sequence eventually reaches 1. However, there are a few exceptions—for instance, if we start with 27, it will take more than 100 steps before the sequence arrives at 1.
The Collatz conjecture is still an open problem in mathematics, which means that no one has yet determined if every starting value produces a sequence which goes to 1. Since no one knows if the conjecture is true or false, there are two possible approaches to the problem: one can either attempt to use a logical argument to show that the conjecture is true, or one can find a counterexample (i.e. a starting number that does not produce a sequence that goes to 1) to show that the conjecture is false.
The first approach is quite difficult, as is often the case with problems in number theory. In general, the more structure a set of objects has, the easier it is to prove results. There just isn’t all that much structure embedded in the positive integers, so it is hard to prove general results. Because of this difficulty, it makes sense to attempt to find a counterexample.
Unfortunately, this, too, has proven to be nontrivial. To date, no counterexample has been found, and a tremendous number of starting values have been tested. As of last month, one project had verified that no initial value less than 260 provided the sought-after counterexample. While this strongly indicates that the Collatz conjecture is probably true, it does not constitute proof, so the search continues.
The Collatz Function
The Collatz conjecture relates to the function \(f\), which takes a positive integer as input, and gives a positive integer as output. This function is defined piecewise (i.e. in two parts) by the formula
\(f(x) = \begin{cases}x/2&\text{$x$ is even,}\\ 3x+1&\text{$x$ is odd.}\end{cases}\)
To a mathematician, an obvious question to ask about this functions is, “Can we extend this to function that is defined on more than just the positive integers?” That is, can we come up with a function \(C\) such that \(C(x) = f(x)\) if \(x\) is a positive integer, but where \(x\) need not be a positive integer?
One possible function is given by
\(g(x) = \begin{cases}x/2&\text{$x$ is an even integer,}\\ 3x+1&\text{$x$ is an odd integer,}\\ 0&\text{otherwise.}\end{cases}\)
This function clearly fits the bill—\(g\) is identical to \(f\) for all positive integers, and \(g\) can take any number, including complex numbers, as input and give a meaningful output. However, \(g\) is boring and, even more unforgivable, it is not a well-behaved function. To throw some jargon out there, \(g\) is not differentiable, nor even continuous.1Intuitively, a continuous function is a function whose graph can be drawn without lifting one’s pencil from the page. That is, there are no holes in the graph. A differentiable function is a continuous function that is smooth, i.e. a function which has no sharp corners or cusps. Continuous and differentiable functions are of great significance to mathematics, and since \(g\) is neither, it is considered ill-behaved. Since it would be nice to have a more interesting, well-behaved function to work with, let us further require that \(C\) be differentiable.
We’re going to get into some pretty heady stuff here for a minute, so if you are intimidated by the notion of differentiable, feel free to skip past to box to the punchline below.
To start, we will define two special functions. The first function, \(\chi_e(x)\) is going to be 1 when \(x\) is even, and 0 when \(x\) is odd. The other function, \(\chi_o(x)\) will be 1 when \(x\) is odd, and 0 when \(x\) is even. Moreover, we are going to define these functions in such a way that they are differentiable.
Before we do this, perhaps we should explain why it makes sense. Consider the function
\(C(x) = \chi_e(x)(x/2) + \chi_o(x)(3x+1)\)
Assuming that \(\chi_e\) and \(\chi_o\) are differentiable, then \(C\) is the sum of products of differentiable functions, and is therefore differentiable itself (that this is true is a result first seen in elementary calculus, then generally proved by advanced undergraduates in mathematics). Of equal importance is the fact that \(C\) and \(f\) agree on all of the positive integers. That is, if \(x\) is a positive integer, then \(C(x) = f(x)\). Finally, \(C\) is defined over whatever domain the functions \(\chi_e\) and \(\chi_o\) are defined, so if we are careful in their construction, we should be able to define \(C\) for all complex numbers.
To define \(\chi_e\), note that \(-1^{x}\) is 1 when \(x\) is even, and \(-1\) when \(x\) is odd. This isn’t quite what we want, but it is close. If \(x\) is odd, then \((-1)^x + 1 = 0\), which is exactly what we want for odd \(x\). Unfortunately, when \(x\) is even, \((-1)^x + 1 = 2\), which is not what we want—it is off by a factor of 2. But that isn’t really problem. By dividing the entire thing by 2, we get the desired result. That is,
\(\displaystyle \chi_e(x) = \frac{(-1)^x+1}{2} = \begin{cases}1&\text{$x$ is even,}\\ 0&\text{$x$ is odd.}\end{cases}\)
If we define \(\chi_e\) in this manner, we get a function that behaves in the manner that we want with regard to parity. However, \((-1)^x\) is imaginary when \(x\) is not an integer. Fortunately, this is not a problem if don’t mind working with complex numbers. Defining \(\chi_o\) in a similar manner, and using \(z\) rather than \(x\) (which is the convention when dealing with complex numbers), we get
\(\displaystyle C(z) = \left(\frac{(-1)^z+1}{2}\right)\frac{z}{2} – \left(\frac{(-1)^z-1}{2}\right)(3z+1).\)
After some significant simplification, and taking advantage of the fact that \((-1)^z\) can be dealt with in terms of trigonometric identities, we finally arrive at our function,
\(\displaystyle C(z) = \frac{1}{4}\left(2+7z-(2+5z)\cos(\pi z)\right).\)
Here’s the punchline: we are going to call the function \(C:\mathbb{C}\to\mathbb{C}\) defined by
\(\displaystyle C(z) = \frac{1}{4}\left(2+7z-(2+5z)\cos(\pi z)\right)\)
the Collatz function. It can easily be verified that if \(z\) is a positive integer, then \(C(z) = f(z)\). For example,
\(C(5) = \frac{1}{4}\left(2+7(5)-(2+5(5))\cos(5\pi)\right) = \frac{1}{4}(2+35-(2+25)(-1)) = \frac{1}{4}(64) = 16,\)
which, given the earlier example, is the expected result. Better still, \(C\) is a continuous function, and is differentiable over the complex numbers. This function is everything that we could possibly want it to be.
The Collatz Fractal
The function \(C(z)\) is a complex valued function which behaves nicely in many respects. Moreover, it is a function that is meant to generalize the Collatz process over the complex numbers. A natural question which arises is, “How does this function behave under iteration?” That is, if we give the function a starting point, then iterate over and over again, what happens?
We have already seen that for many real numbers (specifically, the positive integers that are less than 260), repeated iteration eventually leads to 1, and it is easy to see that after that, the sequence falls into a predictable orbit: \(1\to 4\to 2\to 1\to\cdots\). Thus there are clearly complex numbers that generate have bounded sequences.
It can also be seen that there are complex numbers that do not have bounded orbits. For instance, under repeated iterations, the sequence generated by imaginary unit \(i\) diverges away from the origin at an astounding rate—after just three iterations, the result is so large that the mathematical software Maple considers it to be infinite.
Thus we may divide the complex numbers into two sets: those that generate bounded sequences, and those that do not. In the same way that we defined the Mandelbrot set to be the set of complex numbers that generate bounded sequences under successive iterations of the Mandelbrot function, the Collatz set is defined as the set of complex numbers which generate bounded sequences under successive iterations of the Collatz function. Using basically the same code used to render images of the Mandelbrot set, we can create images of the Collatz set.

Figure 1: The Collatz set, centered at the origin.
In the Figure 1, points that generate sequences that have not escaped after many iterations are black, while points that generate sequences that have escaped are white. In other words, the Collatz set is shown in black. The large black region at the center of the image is at the origin of the complex plane, while the edges of the image are at 5 on the right, and \(-5\) on the left.
The set seems to hug the real axis in complex space. This is not entirely unexpected—assuming that the Collatz conjecture holds, we might expect to find a little blob of black at every integer on the real axis. We seem to see something like that in the image above, though it is not entirely clear what, exactly, is going on. To get a better idea, let us color the complement of the Collatz set (i.e. the white region) using the same kind of coloring algorithm we used for the Mandelbrot set.
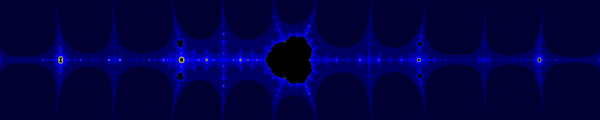
Figure 2: The Collatz set, centered at the origin with escape time coloring.
Figure 2 shows the same region as Figure 1, but with each color representing the number of iterations required before a point is declared to not be a member of the Collatz set. Each of the spikes occurs at an integer on the real axis, which seems to imply that there is something special about the integers. Unfortunately, a complete understanding of the behaviour of this set is equivalent to a complete understanding of the Collatz conjecture (and then some), thus it is unlikely that there is much more that we can say about it.
However it is interesting to note that the Collatz set is, like the Mandelbrot set, a fractal. The boundary is infinitely complex, and there is a great deal of self-similarity that can be seen by “zooming in” on different regions of the fractal.
Finally, on purely aesthetic grounds, a few more images:
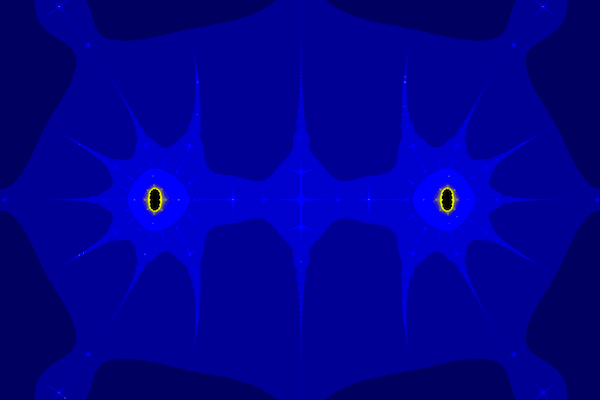
Figure 3: A region of the Collatz set centered near \(25+0i\)
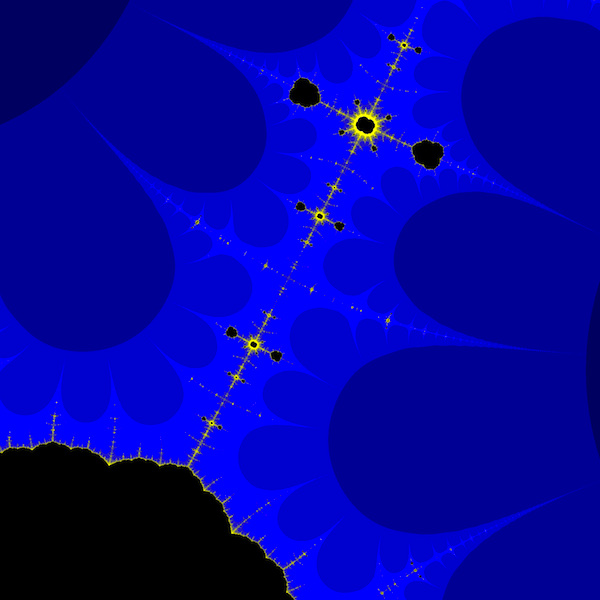
Figure 3: A region of the Collatz set centered near \(0.09+0.42i\)
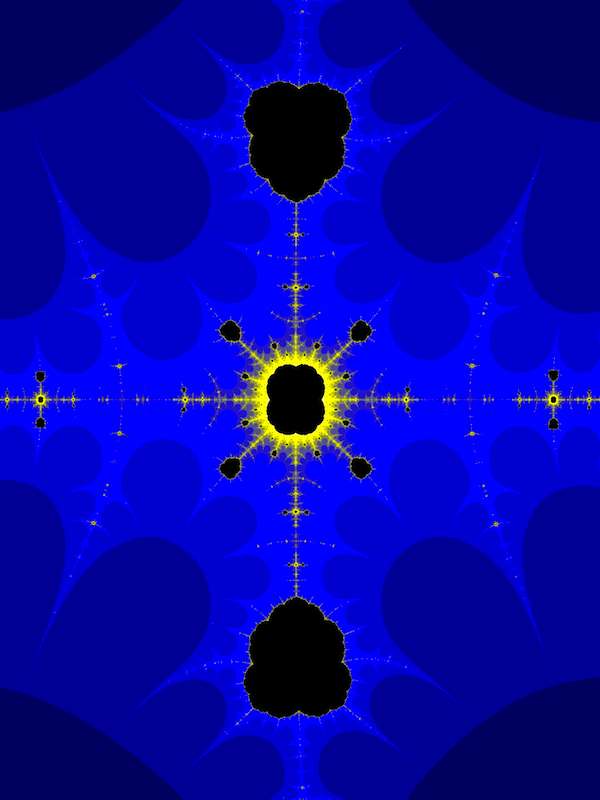
Figure 3: A region of the Collatz set centered near \(-1+0i\)

Interesting! I tried to replicate this and noticed you have a sign error in your first definition of C(z). You have
C(z) = (-1^z + 1)/2 * (z / 2) + (-1^z – 1)/2 * (3*z + 1)
but I think it should be
C(z) = (-1^z + 1)/2 * (z / 2) – (-1^z – 1)/2 * (3*z + 1).
With the first definition, C(5) = -16 and C^n(i) diverges very rapidly. With the second definition, C(5) = 16 and C^n(i) diverges, but not quite so dramatically.
You are correct. My nemesis, the dreaded WRONG SIGN has reared his ugly head once again. I have corrected the post.
Thank you,
xander
Also, I could only get
C(z) = 1/4 * (2 + 7z – (2 + 5z) cos (pi *z))
from
C(z) = (-1^z + 1)/2 * (z / 2) – (-1^z – 1)/2 * (3*z + 1)
if I let -1^z = cos (pi * z). But -1^z = cos (pi * z) – i sin (pi * z).
cos(pi*z) behaves the same on positive integers as -1^z, so I guess the choice is arbitrary. I was just a little confused by the derivation. Using -1^z I get a different fractal that diverges almost everywhere.
Great post! Fun thinking about this.
The general goal was to get a smooth function that behaved in a particular manner over the integers. Since [latex]i\sin(\pi z)[/latex] vanishes over the integers, we can get the behaviour that we want, i.e. [latex]C(x)|_{\mathbb{Z}} = f(x)[/latex] if we drop it. It was sloppy of me to not go over those details. Sorry.
Alternatively, I suppose that we could do a better job of choosing the characteristic functions in the first place. [latex]cos(\pi z/2) = \pm 1[/latex] when [latex]z[/latex] is even, and 0 otherwise; and [latex]\sin(\pi z/2) = \pm 1[/latex] when [latex]z[/latex] is odd, and 0 otherwise. Squaring these gives us the behaviour we want for the characteristic functions, and application of the power reducing formulae will give us the formula I originally gave.
The morals of the story: first, the smooth extensions of functions to larger domains need not be unique; and second, I shouldn’t try to work from three sets of notes at the same time.
Thanks for keeping me honest,
xander