I don’t know a lot about the game Sudoku—I haven’t played that may squares, nor have I ever gotten really into the mathematical study of the game. However, I can certainly understand the attraction: there are a large number of interesting questions that can be asked about Sudoku that are easily stated, but require some pretty nifty mathematics to come to terms with.
Introduction
First, a little background. Sudoku is a is a pen-and-paper game similar to a crossword puzzle. The game board consists of a large square that is broken down into nine smaller squares, each of which is further broken down into nine more squares, which I will call cells. The author of a Sudoku puzzle will fill some number of cells with integers between 1 and 9—these are the “clues” that the player will use to complete the puzzle. The player’s goal is to solve the puzzle by filling in the remaining cells, subject to two constraints: cells must be filled with integers between 1 and 9, and each row, column, and box (3×3 block of cells) must contain each integer between 1 and 9. For example, consider this example from Daily Sudoku:
So what kinds of questions might we ask about Sudoku puzzles?
A Sudoku player might want to know if a particular puzzle can be solved at all, and, if so, if there is more than one solution. Assuming that a puzzle has a solution, the player may want to know if there is an algorithm that can be successfully used to solve the puzzle in an efficient manner. A puzzle author would probably be interested in knowing how many clues he or she is required to include in order to guarantee that the puzzle has a unique solution.
These questions are fairly easy to state—if one understands the rules of Sudoku, then one probably understands the meaning and significance of these questions, and may even have some ideas.
For instance, consider a refinement of the last question: suppose that I am a puzzle author, and I want to create a puzzle that has a unique solution. What is the minimum number of clues that I must provide?
The Logical Approach
Clearly, one clue is not enough—if I provide only one clue, then the player is pretty much free to do whatever they like. Even 7 clues are not enough. If I provide the player with 7 clues, then there are at least two numbers that I am not using—to give an example, suppose that I don’t use 1 or 2 as clues. If a player arrives at a solution to my puzzle, then there is a very easy way to get another solution: change all of the 1s into 2s, and all of the 2s into 1s. Thus a Sudoku author needs to provide more than 7 clues in order to create a puzzle that has a unique solution.
On the other end of the scale, there are examples of puzzles with 17 clues that have unique solutions. Thus it is possible to create puzzles that have only 17 clues and a unique solution. This does not guarantee that a puzzle with 17 clues will have a unique solution (or even any solution at all), but it does mean that the minimum number of clues required for there to be the possibility of a unique solution is at most 17.
Thus far, we have determined that a puzzle with 7 clues will have multiple solutions (if it has any solutions at all), and that there exist puzzles with 17 clues that have unique solutions. Thus the minimum number of clues needed to create a puzzle with a unique solution is between 8 and 17. Now what? Where can we go from here?
Brute-Force
It turns out that this is, in practice, a very difficult question to answer. The reason for this is that we have found ourselves lost in a branch of mathematics called number theory. Number theory deals with questions related to the natural (counting) numbers and the integers. Like our questions about Sudoku, questions in number theory are generally very easily stated, but can be quite difficult to answer. There just aren’t that many tools that can be used to get answers.
Often, when confronted with number theoretical problems, the only way forward is brute force. In the case of our Sudoku problem, the first step might be to see if there are any 16 clue puzzles that have a unique solution by checking every single 16 clue puzzle in existence. Unfortunately, there are over five billion combinations of integers that can fill in a Sudoku square. Checking every possible 16 clue puzzle involves picking one of the five billion solutions, then going through every possible set of 16 clues that could lead to that solution, and making sure that there are no other solutions. If I am doing the arithmetic correctly, this would require checking over 1025 puzzles for unique solutions.
To say that 1025 is a large number would be an understatement. Even the fastest computers in the world would require centuries to work through all of these puzzles. There is no obvious logical argument that gives us an answer to our question, and brute-force is not practical because the space that we have to search is just too big.
Pruning
If we can’t possible examine every possible 16 clue puzzle, maybe there is some way of eliminating a significant number of them. Perhaps there is a large subset of puzzles that are basically identical. To get an idea of what this might look like, consider the game of Tic-Tac-Toe.
Starting with an empty Tic-Tac-Toe grid, the first player can place an X in any of the 9 cells. The next player has 8 possible locations for an O, then the first player has 7 options for another X. This process continues until the board is full. On the surface, it looks like there are
\(9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1 = 362,880\)
games that could be played. This is something of an overcount, as the board does not have to be full in order to declare a winner. For instance, this game is over:
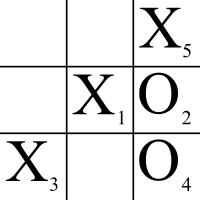
The order in which players place marks on the grid matters, so this has been indicated with subscripts. Note, however, that this game, which is clearly over (X has won), will be counted 24 times, as our original count is of filled Tic-Tac-Toe boards. If we wanted to know how many possible Tic-Tac-Toe games could be played, we would only count the above once, hence we have already eliminated quite a few games from out count.
Moreover, consider these two initial moves by X:
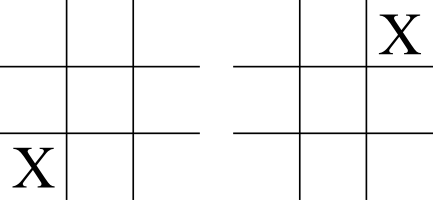
These look like different initial moves, but in terms of playing the game, the are identical. In fact, X only has three choices for an opening move: the center, and edge, or a corner. Due to the symmetry of the game, which corner or edge doesn’t matter—the game is essentially the same. Taking these observations into account, we can arrive at a new count of only 26,830 possible games.1See Steve Schaefer’s website for details of the computation.
This process, i.e. finding and eliminating redundant situations so that they are not counted multiple times, is called pruning. In Tic-Tac-Toe, it is fairly easy to see which boards need not be considered. Is it possible to do the same with our question about Sudoku?
Now, to finally get to the impetus for this ramble, it turns out that the answer is almost certainly yes. In fact, Gary McGuire, a mathematician from Ireland, claims to have done just that. By cleverly pruning the possible 16 clue games, McGuire has shown that no 16 clue puzzle has a unique solution. This means that 17 is the minimum number of clues needed in order for a unique solution to exist. Finding this answer is a remarkable accomplishment. Understanding how to prune the problem space is no mean feat, and conceptualizing in a way that can be programmed into a computer is no less impressive—I’ve skimmed over the paper, and I must admit that I only barely understand what McGuire is doing. Assuming that the solution survives peer review (and there is no reason to suspect that it will not), congratulations are due to Dr. McGuire and his team.