Image Details
As I recently introduced Julia sets into the discussion of fractals and the Mandelbrot set, I would like to spend some time exploring various Julia sets. The first of these is pictured above.
The image shows a region of the complex plane centered at the origin that is about 2.5 units wide and about 1.5 units tall. The Julia fractal shown was generated with the constant \(K=-0.8+0.156i\). To get some idea about how this particular Julia set relates to the Mandelbrot set, I will direct you to Wolfram Alpha, which as some nice tools for dealing with all kinds of mathematics.
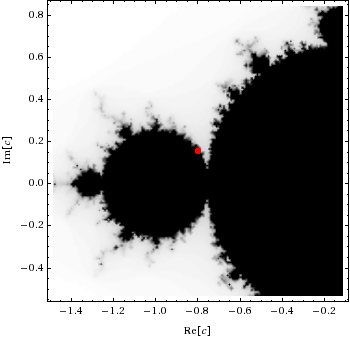
The above image should be fairly familiar by this time—it is a part of the Mandelbrot set. The red dot indicates the location of the constant K. It turns out that this K is not in the Mandelbrot set, but it is very close to the boundary. Because of this, we can use the same escape time coloring algorithm to generate some very pretty images.

It is also interesting to note how the shape of the Julia set mirrors the shape of the Mandelbrot set near the coordinates of K. The same kinds of looping, swirling, and radial structures that are seen near Seahorse Valley in the Mandelbrot set are seen in a Julia set generated with a constant from the region. I don’t claim to entirely understand the relationship, but I find the similarity of form fascinating.


That is indeed a very pretty one. It’s all starting to make sense to me (key word = starting)… and in the meantime, makes for a very relaxing desktop background!