The Mandelbrot Set Series:
This post is the third in a series on the Mandelbrot set. The Mandelbrot set resides upon the complex plane. This means that in order to look more closely at the Mandelbrot set itself, we need to first get a handle on the complex plane. That is the topic of this post.
- Part I: Fractals
- Part II: Exploring the Mandelbrot Set
- Part III: Complex Numbers
Imaginary Numbers
If you have made it as far as algebra, you have encountered many kinds of numbers. You probably started by learning about natural numbers in kindergarten, although you probably called them whole numbers or counting numbers. At some point, you learned about fractions. Fractions are not whole numbers, but belong to a larger class of numbers called rational numbers 1Rational refers to the fact that the numbers can be expressed as a ratio of natural numbers. Think rational. It has nothing to do with the numbers being insane or unreasonable, or anything like that.. A little while later, probably while talking about the measurements of various geometrical figures, you learned about irrational numbers. Things like \(\sqrt{2}\) and \(\pi\), which cannot be represented by a terminating, non-repeating decimal. You also almost certainly learned about the integers, which consist of positive and negative whole numbers, and zero.
The imaginary numbers are simply one more class of numbers. The name is a bit unfortunate, as imaginary numbers are really no more nor less imaginary than any other class of number. Unfortunately, when they were first described by mathematicians, there was an element of disbelief and suspicion, and the name stuck.
In general, each class of numbers serves to answer a question that other classes of numbers cannot completely answer. For instance, rational numbers are useful for dividing objects into discrete pieces (which can’t be done with whole numbers alone), and negative numbers are useful for balancing a checkbook (which cannot be done with positive numbers alone). Imaginary numbers turn out to be the solutions to a certain kind of equation. Specifically, imaginary numbers are required in order to solve equations like \(x^2+1=0\).
In the above equation, we would normally solve by subtracting one from each side, then taking the square root. This gives us \(x^2=-1\Rightarrow x=\sqrt{-1}\). Just as we cannot discuss what happens when we divide an apple into two pieces using only whole numbers, we cannot adequately solve the above equation using only real numbers 2The real numbers are a class of numbers containing all of the rational and irrational numbers. All of the integers are contained within the rational numbers, and all of the whole numbers are integers. This means that the real numbers account for practically all of the numbers that we encounter in our day-to-day lives.. There is no real number that, when squared, gives us \(-1\).
This is where imaginary numbers come into play. We start by defining the imaginary unit \(i\). \(i\) is a number that, when squared, gives \(-1\). As \(i^2 = -1\), \(i\) is a solution to the above equation. By extension, every equation of the form \(x^2 = -a\), where \(a\) is positive number, has a solution of the form \(x=\pm i\cdot\sqrt{a}\).
It is interesting to note that imaginary numbers of the form shown above can be placed on a number line which looks very much like the number line that is often introduced in elementary school. To the right, we have positive imaginary numbers, and to the left, we have negative imaginary numbers:
We can add and subtract imaginary numbers just like we add and subtract real numbers. For instance, \(3i+2i=5i\). However, multiplication works a bit differently. As \(i\cdot i\) is defined to be \(-1\), the product of two imaginary numbers is going to be a real number. For example, \(4i\cdot 3i = (4\cdot 3)(i\cdot i) = 12\cdot (-1) = -12\). This should strike us as a little unintuitive, as we are used to multiplying two numbers on the number line and getting another number on the number line.
Complex Numbers
We have already seen that imaginary numbers behave a little oddly when multiplied: the product moves off of the imaginary number line, and appears on the real number line. Clearly, there is some relationship between imaginary numbers and real numbers. Graphically, we might represent this relationship as a coordinate system. For instance, we can keep our real number line horizontal, and turn the imaginary number line 90 degrees, like this:
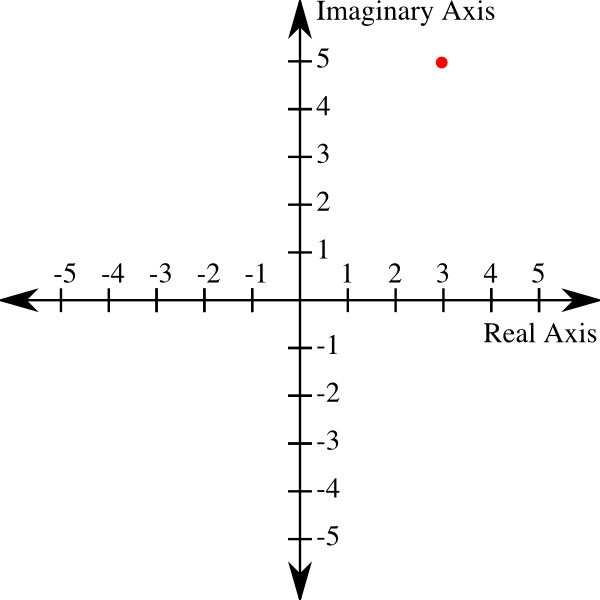
This is the complex plane. Every point on this plane has a real coordinate, and an imaginary coordinate, which can be expressed as a tuple (ordered pair) like this: \((3,5)\). In this tuple, 3 is the real coordinate, and 5 is the imaginary coordinate. We could plot this point just as we would plot a point on the Cartesian plane (a plane with \(x\) and \(y\) axes).
Numbers that have a real and imaginary component are called complex numbers. They can be expressed as a tuple, as above, or they can be expressed as the sum of the real and imaginary components. The point above could also be written as \(3+5i\).
Of course, now that we have complex numbers, we need a way of working with them. That is, we need to define how basic operations work. In order to work with the Mandelbrot set, we are going to need multiplication and addition, so let’s define those two operations.
There is a fair bit of notation in the box below, and if it gets to be too much, feel free to skip it. However, I think that it is worthwhile to read through it, and try to come to terms with it.
Addition is pretty easy: we simply add in a component-wise fashion. Abstractly, suppose that we have two complex numbers, say \(X=a+bi\) and \(Y=c+di\). Then \(X+Y = (a+c)+(bi+di)\). Simplifying this, we get \(X+Y = (a+c)+(b+d)i\). To give a more concrete example, consider \((5+3i)+(7+2i)\). Adding component-wise, we get \(12+5i\).
Because of the imaginary components, multiplication is a little bit trickier. Using the same \(X\) and \(Y\) from above, we have \(X\cdot Y = (a+bi)\cdot(c+di)\). The multiplication works like multiplication with any polynomial—we apply the distributive property of multiplication over addition 3In many American schools, a simplified version of this rule, called FOIL (first, outside, inside, last) is used for polynomials of the kind seen here. Doing this, we get \((a+bi)\cdot(c+di) = ac+adi+bci+bdi^2\). This can be simplified a little. First, recall that, by definition, \(i^2=-1\). This means that we can simplify \(bdi^2\) as \(-bd\). Second, we group like terms, giving us a final result of \((a+bi)\cdot(c+di) = (ac-bd)+(ad+bc)i\). Again, providing a more concrete example: \((5+3i)\cdot(7+2i) = 29+31i\).
The long and short of it is that complex numbers can be added and multiplied (and, by extension, subtracted and divided) just like any other number. Addition is very straight-forward, but multiplication requires just a little bit of work.
Conclusion
In the course of mathematics, it was discovered that certain kinds of equations did not have solutions within the set of numbers that mathematicians were used to dealing with. To solve these equations, mathematicians had to invent imaginary numbers, which could be thought of as the square roots of negative numbers.
Imaginary numbers and real numbers can be combined through addition in order to create a set of numbers called complex numbers. Complex numbers can be added and subtracted, and multiplied and divided, and generally behave like “normal” numbers, though there are a couple of tricks required in order to work with them.
Perhaps most important to our discussion of the Mandelbrot set, complex numbers can be graphically represented as points on a plane. A point’s horizontal position relative to the origin (i.e. the zero point) represents its real component, while its vertical position relative to the origin represents its imaginary component. As we move forward, this graphical representation of complex numbers will be significant.
