I have a much younger sister who is currently in high school. In her mathematics classes, she has started to get into trigonometry and trigonometric identities. A few nights ago, she had some questions, which got me thinking once again about how mathematics is taught.
The questions that my sister was being asked to answer were similar to the following:
You are given that \(\sin(\theta) = \sqrt{3}/2\) and \(\cos(\theta) = 1/2\). Find
- \(\csc(\theta)\)
- \(\tan(\theta)\)
- \(\sin(90-\theta)\)
These problems are not terribly interesting, but they do serve the purpose of getting the student to work with trigonometric identities, and they can serve to help students get a feel for relationships between those identities. However, these exercises are utterly worthless if the student is not introduced to the identities in a productive manner.
From my own experience, and from questioning my sister about her math class, I imagine that the trigonometric identities were introduced as a list of equalities that the students needed to memorize. They were given the mnemonic “SOH CAH TOA,”1For those unfamiliar with this mnemonic, it is a way of remembering the definitions of the three basic trigonometric functions as they related to right triangles. The sine is the ratio of the opposite side to the hypotenuse, thus “SOH” stands for “sine is the length of the opposite side over hypotenuse.” and a list of further trigonometric functions.
The task of the student then becomes looking up identities in a table and hoping that they make no mistakes in substitution. This is ridiculous, and does nothing to foster intuition. This creates students who can push the buttons on a calculator, but who cannot actually solve problems.
When my sister read the problem to me, my first instinct was not to run to a table of identities and start looking for useful information, but rather it was to start drawing triangles. So I drew a right triangle on my whiteboard, and started labeling it.
First, we are curious about the sine and cosine of \(\theta\), so there must be some angle which measures \(\theta\) on the triangle.
Next, we can start filling in other things that we know. For instance, the sine tells us that if the length of the side opposite \(\theta\) is \(\sqrt{3}\) units long, then the hypotenuse is 2. So we can label these two sides. With this information, we can apply the Pythagorean theorem to find the third side, or we can use the definition of the cosine in the same way that we did the definition of the sine.2It is important to note here that there are several different ways in which we can find the remaining side. One of the joys of mathematics is that there are often many tools that can be used to get the same job done. This means that we can use the tool with which we are most comfortable, and if we think we did something wrong, we can pull another tool out of the box and check our work. In either case, we find that the third side must be 2 units.
At this point, we know how long all three sides are, and we know the measures of two of the three angles (one angle is \(\theta\), and the triangle is a right triangle, so another angle measures 90°). We probably want to find the measure of the last angle. For this, we have to remember that all of the angles in a right triangle must add up to 180°. We have two angles which add up to 90+\(\theta\)°, so the remaining angle must be \(90- \theta\)° (by application of a little bit of algebra). We now know everything that there is to know about our triangle.
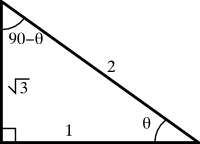
Now that we know all that there is to know about a triangle that wasn’t even a part of our original exercise, what do we do?
Finding \(\sin(90-\theta)\) is actually pretty trivial now. When we look at our labeled triangle, we see the quantity \(90- \theta\) as the measure of one of the angles, which means that we just need to know the length of the opposite side and the hypotenuse to calculate the sine (remember, “SOH CAH TOA”). That gives us \(\sin(90-\theta) = 1/2\).
We could have figured this out by looking up \(\sin(90-\theta)\) in a table of identities, and we would have discovered that \(\sin(90-\theta) = \cos(\theta)\), but where is the insight? How does that help us gain an intuition for how the functions are related?
By drawing the triangle, we can see that the two non-right angles of a right triangle are related: they add to 90°. This means that on any triangle there is a relationship between the sine of one angle and the cosine of the other. The geometry of the problem gives us some insight into why it works.
Moving on to the tangent, our same table of values might state that \(\tan(\theta) = \sin(\theta)/\cos(\theta)\). However, using our figure and “SOH CAH TOA,” we can easily calculate the tangent as \(\sqrt{3}\). We just need to find the ratio of the opposite to the adjacent. Sure, we have to memorize a mnemonic, but it is the same simple mnemonic that we already have memorized.
Thus far, we have done everything required of us without needing to memorize anything beyond a simple mnemonic. We have not needed to look anything up in a table, and we have not needed a calculator. With a set of very simple facts and definitions, we were able to solve two of the three problems.
The last problem hinges on what the definition of the cosecant is. For this one, we are going to have to know something else, namely that \({\rm csc}=1/{\rm sin}\). We either have to commit this to memory, or use a table to look it up. However, our picture still gives us some insight. The secant, cosecant, and cotangent are all related to the sides of the triangle, as well. The only difference is that the hypotenuse goes on top (or the adjacent side, in the case of cotangent). Where a unit fraction like \(1/\sin\) might be a little imposing, simply flipping a fraction is a much less painful process.
Once again, going back to basic definitions and drawing a picture helped.
In short, teaching students to memorize a bunch of facts or tables is not the best way to teach mathematics. Certainly, there are times where it is unavoidable—for instance, I cannot see a way of teaching trigonometry without having students memorize the definitions of the basic trig functions—but such memorization should be kept to an absolute minimum.
Ultimately, mathematics is about finding ways to generalize our knowledge. The fact that \(\tan=\sin/\cos\) is not the important lesson here; the important lesson is that little pieces of information can fit together like puzzle pieces, and that with only a little bit of data, we can create a more complete picture of a larger whole. This applies to trigonometry, to arithmetic, to calculus, and to a much wider range of thinking that transcends mathematics. It is the process that is important, not the result.
