Mathemagic

I love magic.

A friend of mine, who works as a professional magician, introduces one of her tricks by explaining that she was trained as a dancer. In dance, she says, the performers want the audience to see everything that they are doing. Dance is an expressive art form where movements are often exaggerated so that the audience can see every detail. Magic, by contrast, is secretive. Magicians use movement to conceal what they are doing, so that the audience is surprised by what happens, and leave a performance thinking, “How did they do that?”

This means that magic can be enjoyed on multiple levels. On one level, the audience can appreciate having the wool drawn over their eyes. Good magic creates mystery. How did that curious, little man fit into that curious, little box? What happened to him when the box was smashed? When the box was reassembled, where did the curious, little man go, and where did that gorgeous woman come from? What is going on here!?

At its most basic, the audience can chew over these magical mysteries.

Then, after seeing the same trick several times, an astute observer might begin to figure out how a trick works (this task is sometimes made easier when the magician’s daughter lets slip a minor trick or two). There are some people that might feel that knowing the trick spoils the experience, but I am forced to disagree with them. When one knows the trick, there is no mystery anymore, but it can still be appreciated as any other stagecraft is appreciated. One can admire the technical skill of the performers or the beauty of movement on display.

In a sense, knowing the trick is like knowing the meaning of the word “Rosebud” in Citizen Kane. The meaning of this enigmatic word is known only to a character who dies before the film even begins. It is only in the closing shot that the audience is let in on the secret. When watching the film for the first time, a viewer might be in a state of suspense, sitting on the edge of their seat, trying to work out the meaning of the phrase. However the film stands up to repeated viewing, thanks to the phenomenal talent that went into its production.

Watching a trick for the hundredth time is like watching Citizen Kane for the hundredth time: the experience isn’t about the mystery any more, but about finding subtle nuances that you never knew were there.

In short, I love magic.

“But!” you may ask, “what does this have to do with mathematics?”

Mathematics and magic are deeply linked. At its heart, good math, like good magic, is about puzzles. In magic, the puzzles revolve around how particular tricks are done. In math, the puzzles revolve around what kinds of statements are true.

For instance, consider a map of the continental United States. With just four different colors, we can color in each state in such a way that no two adjacent states are the same color. But if we use only three colors, there are going to be at least two states that share a common border and a color. There is no way to color the continental US with only three colors such that no two states that are the same color share a border.

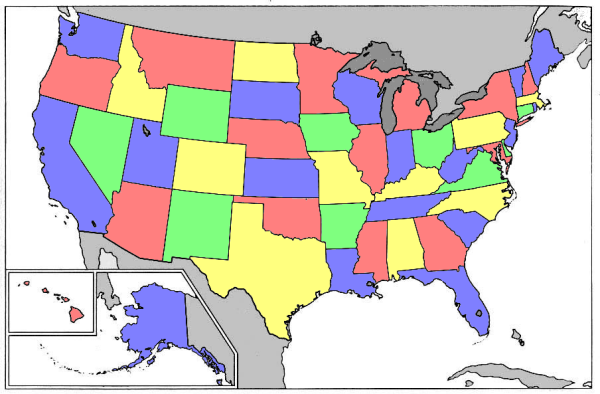
More generally, suppose that we take a piece of paper, and divide it into regions in the same way that the US is divided into states. Is there any way of knowing how many colors we will need?

This particular problem puzzled mathematicians for more than 100 years before anyone came up with a really good, convincing solution. Mathematicians thought that any map could be colored with only four different colors, but actually proving it turned out to be quite difficult. In an attempt to either prove or disprove that four colors were sufficient, mathematicians drew millions of maps, and employed some crazy mathematical tricks, but were not able to definitively say, “Aha! It takes only four colors to color a map!”

In the same way that an audience member watching a magic performance knows that there must be some trick, but she can’t figure it out, mathematicians knew that there must be some kind of trick, but they just couldn’t figure it out.

In this sense, mathematicians enjoy their work for much the same reason that audiences enjoy magic: there are mysteries to be solved and knots to untangle.

But mathematics and magic also share some more practical ties. I recently went to a performance where the magician asked an audience member to give him a number at random. He then filled in a 5×5 grid with numbers as quickly as he could. It took him maybe 30 seconds—he was writing so fast that it didn’t look like he was taking much time to think about what he was doing. He then demonstrated that the sum of every row was the number that the audience member called out. The audience was impressed. He went on to demonstrate that the sum of every column was also the magic number. The audience was even more impressed. Finally, he added up the diagonals, and they also summed to the magic number. The audience was blown away.

The mystery of this trick is how quickly the magician was able to fill out his grid of numbers. Most people cannot add 5 two-digit numbers in their head in less than a second, let alone write down 25 numbers in 30 seconds such that various arrangements sum to the same amount.

In reality, the magician probably was not adding numbers together in his head at a phenomenal rate. It is almost certain that he was not some kind of mathematical savant. Instead, he was probably employing the properties of a magic square. Take, for example, this 4×4 square:

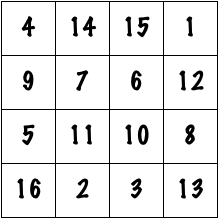
This square is special. The numbers in each row add up to 34, as do the numbers in each column, and each diagonal. As an added bonus, the numbers in the square are the numbers 1 through 16. I invite the readers to check this for themselves. If the magician has a 4×4 grid to fill, has memorized this square, and an audience member shouts out 34, then life is golden. He simply writes down the numbers as they appear here, and he is done. The trick is nothing more than some clever memorization.

But what happens if the audience member is squirrelly, and picks some other number? Well, there are a couple of things that can be done. The magician could add some quantity to every number in the grid. If the same quantity is added to everything, the magical properties of the square will still work out. For instance, say I add 1 to every entry. I would get the following magic square:

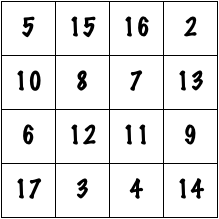
Again, I invite the readers to check that each row, column, and diagonal adds to the same number. In this case, all of the numbers from 2 through 18 are used, and the “magic constant” is 38 (all of the rows, columns, and diagonals add to 38). Every time 1 is added to each number, the magic constant goes up by 4. So if the audience member shouts out any number that can be expressed as 34 plus some multiple of 4, the magician is in luck. These numbers would include 38, 42, 46, 50, 54, and so on.

For instance, if an audience member calls out one of these numbers, say 50, then all the magician has to do is a quick subtraction (\(50-34=16\)), and a quick division by 4 (\(16\div 4=4\)). Then magician has to write down the memorized grid from above, remember to add 4 to each entry as she works. If she paid attention in elementary school, and learned her multiplication tables, this shouldn’t be too hard. It may slow her down a little, but not enough to ruin the magic for the audience.

But what if some other number is selected? Well, there is at least one more trick that the magician could use. Suppose that an audience member calls out the number 35. The magician can get the required square by adding 1 to just four squares:

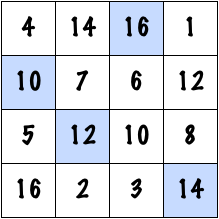
Once again, check the result for yourself. This trick has a small disadvantage, the magician is no longer using a series of 16 numbers that all come in a row. In this case, several numbers are repeated. For instance, the number 14 now appears in the top row, and in the third row. This makes the trick a little bit less amazing, as the numbers being used are neither unique nor in a series. On the other hand, if you were watching it live and didn’t know what was going on, I would be willing to be that you would still be pretty impressed.

Thus far, we have seen how we can add something to every number to change the magic constant, and how we can alter just a few numbers to change the magic constant. By using both methods at the same time, any number can be used as a magic constant. For instance, take 71.

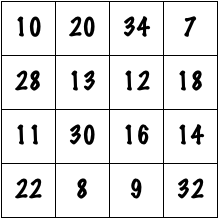
First, we note that \(71-34=37\). We could think of 37 as \(9\times 4 + 1\), or as \(8\times 4 + 5\), or even as \(6\times 4 + 13\). A magician who has been practicing this trick would probably be able to do these computations in her head pretty quickly, and any one of these computations gives the magician all of the necessary information to make the square. First, the magician would consider the number that is multiplying 4. For instance, take the last example, where 4 is multiplied by 6. As the magician writes out the magic square, she would add 6 to every number as she writes it down, except for the four squares highlighted above. When the magician got to those squares, she would add 6, then add 13 more (for a total of 19). The final result would look like this:

While constructing any magic square on the fly in front of an audience is by no means an easy task, the two little tricks above are enough to make the task much easier. Moreover, these tricks can be used to make 5×5 magic squares, or 6×6 magic squares, or even larger magic squares. They only require that the magician memorize the initial layout, and the appropriate places to alter numbers. What was once the impossible act of a savant is now merely very difficult.

Magicians the world over have thousands of little mathematical tricks up their sleeves. To a magician, mathematics can be a very practical tool for giving audiences an encounter with the impossible.

But, perhaps more importantly, this trick forced me, as a member of the audience, to think. In the end, both magic and mathematics present us with problems that we are compelled to think about. They dare us to find solutions, and taunt us until we finally unravel the mysteries, only to reveal that each new solution is only the starting point of another problem.