Image Details
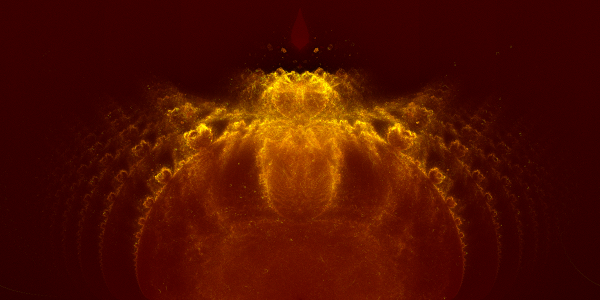
Yet another nebulabrot rendering. This image is the result of applying the nebulabrot technique to the rational function
\(z_{k+1} = \displaystyle\frac{z_n^3}{z_n^2+1} + z_0\).
For those that are interested, the original rendering process produced four images. The lowest layer (representing “high energy” points in the complex plane) set an escape threshold of 0 to 200 iterations, and captured 800 million exposures. This layer took about an hour to render on my laptop (a device that was not really designed for intense scientific computing, but which seems to get the job done).
The highest layer (representing very “low energy” points in the complex plane) had an escape threshold of 5,000 to 25,000 iterations, and captured about 12.5 million exposures. This layer took about 100 hours to render. All four layers were rendered at 9600 by 9600 pixels.
The layers were then combined using GIMP. The brightness was adjusted to pull out details, and a small Gaussian blur was added to smooth the final image a bit. Each layer was colored in a manner that was meant to be aesthetically pleasing, then combined using the additive layer mode. Finally, the image was scaled by 50% as a poor-man’s anti-aliasing method. The result can be obtained by clicking the above image.