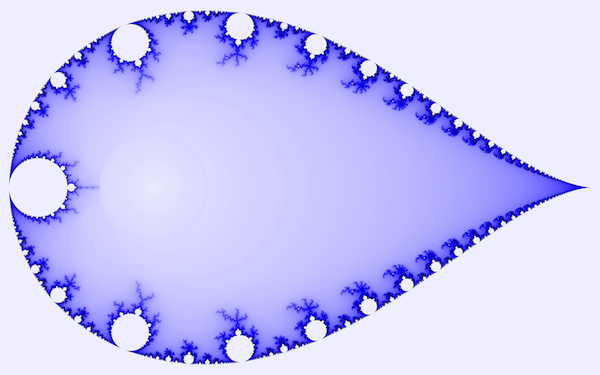
Image Details
This is actually an image of the normal, everyday, run-of-the-mill Mandelbrot set that I first introduced last year. However, there is one small alteration. Before applying the iteration function, each point on the plane is mapped to its inverse. For instance, the point \(0.5+0.5i\) is mapped to \(1.0-1.0i\). Note that
\((0.5+0.5i)(1.0-1.0i) = 0.5 – 0.5i + 0.5i – 0.5i^2 = 1,\)
hence the two points are inverses, as they multiply to 1.
This process of mapping points to their inverses has the effect of (more or less) turning the Mandelbrot set “inside-out.” Now the large whitish region that surrounds the image is made up of points in the Mandelbrot set, while the more colorful regions are actually outside of the set. What this means is that we should still be able to find some of the regions of interest which have been identified in previous posts.
For instance, this image contains a seahorse valley. If you look very carefully at the leftmost portion of the larger image (linked above—approx. 11.7 MB), you should be able to spot it. The seahorses are lined up on the left side of the valley. On the other end of the image, trailing off to point, there is a parade of elephants. Other recognizable features may present themselves, though the resolution of the image and the number of iterations may limit our ability to actually spot them.