Have a quick look at the figure below:

Believe it or not, that figure is a circle.
To understand why this is, let us first leave the world of mathematics for a moment, and imagine instead a deck of cards. There are perhaps thousands of games that can be played with a deck of cards, each one having its own rules and vocabulary. For instance, consider three cards:

In a game of poker, these three cards would part of a hand of five cards. By themselves, they constitute a three-of-a-kind, and form a reasonably strong hand—three sevens beat a pair, for instance. In a game of cribbage, these same three cards are not a three-of-a-kind. Instead, they would be called a pair royal, and would peg six points on the board. In a game of pinochle, these three cards wouldn’t even appear—the lowest ranked card in a pinochle deck is a 9. If we were playing pinochle, we could claim that these three cards don’t even exist! They are exactly the same three cards, but they have very different interpretations depending upon the context.
In this sense, mathematics works in a manner similar to a deck of cards and a book of rules. There are various mathematical creatures that look the same, but are described differently depending upon the rules that are being used.
One particular branch of mathematics—topology—deals with the rules for describing different kinds of spaces. While the technical definition is a bit abstract, for the purposes of this discussion, we can think of a space in an intuitive manner: a space is the environment in which the points and lines from high school geometry live. For instance, a two dimensional space might be a plane that extends to infinity in all directions, and which is populated by points, lines, triangles, and other flat figures.
In such a space, we might want to know how far apart two objects are. To a mathematician, this can be a relatively interesting question, the answer to which comes down to what we mean by distance.
In high school geometry, we were taught that the distance between two points is a straight line. Given two points on a plane, we could get out a ruler, place the 0 at one point, line up the ruler with the second point, and read a distance. A straight line can be drawn between any two points, and their distance from each other is simply the length of that line.
So far, this seems pretty straightforward.
Unfortunately, the real world doesn’t always let us travel in a straight line. Of course, mathematics is an abstraction, and it doesn’t have to match up with what goes on the real world, but sometimes real situations can give us new and different rules to play by.
This is the neighborhood I grew up in:
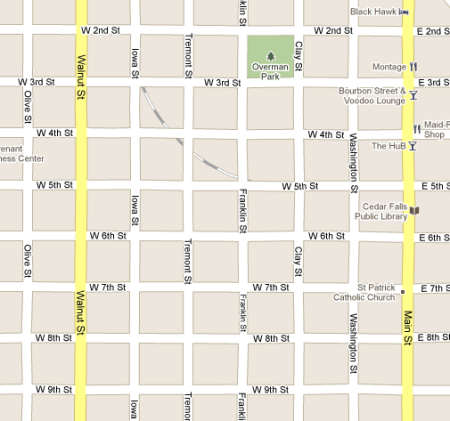
Notice that all of the streets run in a grid pattern. If we wanted to go from Overman Park to the public library, we would have to walk or drive on the roads—it would not be possible to travel in a straight line. Aside from the fact that we would probably be trespassing, there are physical barriers like buildings and fences. It doesn’t make sense to talk about a straight line distance.
Instead, we might use a different kind of distance: the city block metric, or Manhattan distance. When we measure distances on a grid like the one above, we have to travel east or west a certain distance, then north or south a bit farther. To get from the park to the library, we would first travel east on 3rd Street for two blocks, then south on Main Street for anther two and a half blocks. The total distance is about four and a half blocks.
Using the distance formula that we learned in high school, we might calculate the straight-line distance between those two places as about 3.2 blocks. Using two different methods for measuring distance, we get two different results.
Again, this shouldn’t be surprising.
Here is where things start to get a little weird: many of the facts that we learned in high school geometry were based the idea that distance is measured with a straight line. If we change the way that we measure distance, there are many other things that are going to change as well.
To provide a single example, think about a circle. In geometry, a circle is made up of all of the points that are a given distance from the center. If we use the straight-line distance, then we get the round figure that we all know and love. But what happens when we measure distance using the city block metric?
We start by placing a point on the plane, and calling that the center of our circle. Starting at the center of the circle, we travel out a specific distance. As we can only go north, south, east, and west, we trace distances along the dashed lines, as shown:
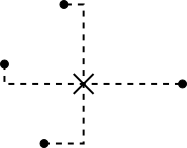
Adding more points to the figure, we get something like this:
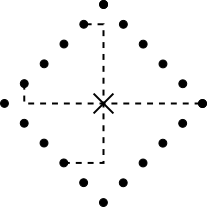
By filling in all of the gaps, we get the figure which started the current discussion:

In this figure, all of the points on the black lines are the same distance from a center point, as measured using the city block metric. Because a circle is defined as the set of points that are all the same distance from some point, this figure must be a circle!
Just as the name and value of a certain collection of cards depends upon the rules of the game being played, the description of a particular geometric figure depends upon the space in which that figure lives. In the space described by high school geometry, that figure is a square (rotated 45° from the “usual” orientation, but a square none the less); in a space where we have to travel in one of four cardinal directions, like a city with roads laid out on a grid, that figure is a circle. It simply depends on how you look at it.
