There was a time when I thought I was going to be an archaeologist. In fact, I nearly completed a bachelor’s program in anthropology, and I spent several summers working for the BLM and Forest Service conducting archaeological survey and excavation. While I eventually moved away from the social sciences and into mathematics, I still have an abiding interest in archaeology, and often think like an archaeologist.
For instance, I am fascinated by material culture—I love the various things that people use in order to carry their daily tasks. I think there is value in learning to use tools that are now obsolete, but which were once vital. In this spirit, I recently picked up an abacus.
Of course, now I have to figure out how to use the damn thing.
History
An abacus is a kind of calculator, similar to the four function calculators that are used in many elementary school classrooms. Abaci are designed to mechanize the processes of addition, subtraction, multiplication, and division in order to quickly perform arithmetic with few errors. They were probably initially developed by merchants in Asia or the Middle East in order to speed transactions along, and are still commonly taught and used in some parts of the world. 1http://faculty.philau.edu/londonm/history/abacus.htm 2http://www.math.wichita.edu/history/topics/calculators.html#abacus
While there are many different kinds of abaci, which come from diverse parts of the world, the general form remains relatively constant. Most abaci consist of a wooden frame which contains several rows of beads strung on stiff wires. A Russian abacus has ten beads on each wire, with one or two wires containing four beads in order to calculate quarter ruble and quarter kopek quantities. The abaci used in many Western classrooms generally have 10 beads on each wire. The Japanese abacus has two decks of beads on each wire—one rank contains four beads, and the other a single bead. 3http://en.wikipedia.org/wiki/Abacus
The abacus pictured above is a Chinese abacus. Like the Japanese abacus (which was based on the Chinese abacus), it has two decks of beads. The lower deck has five “earth beads” on each wire, while the upper deck has two “heaven beads” on each wire. There is evidence that this form of abacus was in use in China as late as 1,000 years ago, though the actual date of invention is unknown, and it is possible that the Chinese abacus is as much as 2,000 years old. 4http://en.wikipedia.org/wiki/Suanpan
Reading the Abacus
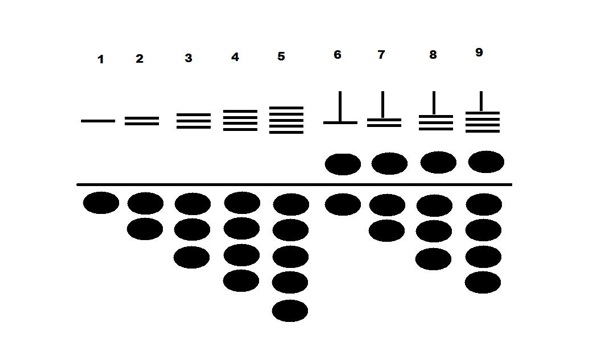
Chinese counting rods (a kind of numeral) use a combination of horizontal and vertical lines. Each numeral consists of two sets of lines. Each line in the bottom set has a value of 1, and each line in the top set has a value of 5. The value of a numeral is found by adding the values of the top and bottom lines. For instance, 7 is represented by 𝍯 (two horizontal lines with a value of 1 each, plus one vertical line with a value of 5). 5http://en.wikipedia.org/wiki/Counting_rods
Each wire on the abacus is read in a similar manner. The value of the wire is equal to the sums of the values of the beads on the wire. Beads in the lower deck are worth 1 each, beads in the upper deck are worth 5 each, and only beads that have been pushed against the beam (the divider between the two decks) are counted. Thus any wire in the abacus can be read as a single number, and compared to a Chinese rod numeral, or to a modern Hindu-Arabic numeral.
For the rest of this post, we are going to be using an idealized abacus.
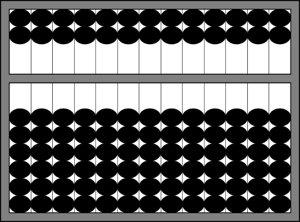
In the image above, the abacus is showing a value of zero. All of the beads in the lower deck are at the bottom of the frame, and all of the beads on the upper deck are at the top of the frame. This abacus has been cleared, and is ready to be used.
Numbers are represented on an abacus using the same kind of positional system that we are familiar with in the West. Each wire of beads represents a place value, i.e. ones, tens, hundreds, thousands, and so on. While the position of the ones place is arbitrary (in order to allow the abacus to represent decimals), we will put the ones on the farthest wire to the right. The next wire will represent tens, then hundreds, &c. Under this system, 2,718 would be represented as
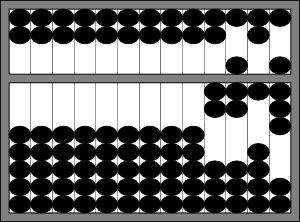
In the ones place, three beads from the lower deck and one bead from the upper deck have been moved to the beam; in the tens place, one bead from the lower deck has been moved to the beam; and so on. The digits are read from left to right, giving us a value of 2 thousands, 7 hundreds, 1 ten, and 8 ones (the number 2,718).
Addition and Subtraction 6Green, Paul. How to Use a Chinese Abacus: A Step-By-Step Guide to Addition, Subtraction, Multiplication, Division, Roots, and More. (Morrisville: Lulu,2007). 7http://www.ee.ryerson.ca:8080/~elf/abacus/leeabacus/bagley/ 8http://webhome.idirect.com/~totton/abacus/
Being able to read numbers off of an abacus is nice, but is not a terribly useful skill by itself. The real power of the abacus comes when we try to perform computations.
In order to add on the abacus, we need to be able to do a very little bit of mental arithmetic. Specifically, we need to be able to add to either 5 or 10 in our heads. Basically, we need the facts \(1+4=5\), \(2+3=5\), \(1+9=10\), \(2+8=10\), \(3+7=10\), \(4+6=10\), and \(5+5=10\). If we can do this, everything else is purely mechanical.
Basic addition works as we would intuitively expect. Given two numbers that we want to add, we register one number on the abacus, then add the second number by moving beads on the appropriate wire. Consider \(8231+458\). First, we clear the abacus and register the larger number on the abacus (the red beads indicate which ones have moved):
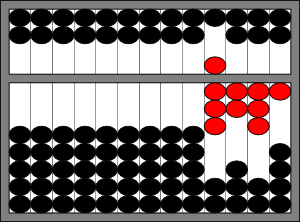
Then, starting on the left and moving to the right, we add the second number:
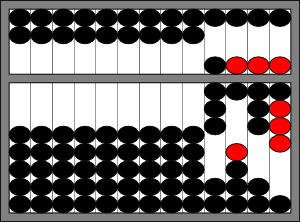
Starting in the thousands place, there is nothing to add. Then we move to the hundreds place, where we want to add 4. There are not four beads in the lower deck, so we need to use one of the addition facts from above: \(1+4=5\). Rearranging this slightly, we find that \(4=5-1\), which implies that we need to add 5 to the upper deck (move one bead to the beam), and subtract 1 from the lower deck (move one bead away from the beam). In the tens place, we move one bead on the upper deck to the beam, and in the ones place we move one bead from the upper deck and three beads from the lower deck to the beam. We can now read the result from the abacus: 8,689.
That’s all well and good, but what do we do if there are not enough beads on a particular wire? Just like in elementary school, we are going to have to carry something. Consider the problem \(18+9\). First, register 18 on the abacus:
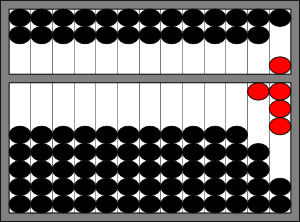
To add 9, we start in the tens place. As there is nothing there, we can move to the ones place. Unfortunately, there are not enough beads. In order to complete the operation, we need to remember another of our arithmetic facts: \(1+9=10\). This implies that \(9=10-1\). So in order to add 9, we will subtract 1 from the ones wire, and add 10 to the tens wire. The means moving one bead on the lower deck of the ones wire away from the beam, and moving one bead on the lower deck of the tens wire to the beam.
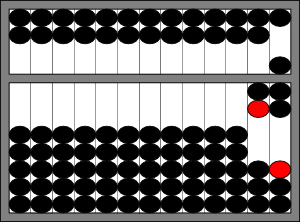
The result, 27, can now be read from the abacus. As a final example of addition, consider \(9,999+77\). Again, start by registering the larger number:
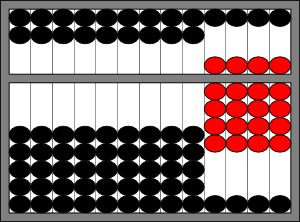
Next, we need to add 5 to the tens place. Unfortunately, there are not enough beads to do this. So, recalling that \(3+7=10\Rightarrow 7=10-3\), we are going to try to add 10 in the hundreds place (one bead from the lower deck), and subtract 3 from the tens place (three beads from the lower deck). The tens place is easy, but we don’t have enough beads in the hundreds place to do what we want. 9There is a method for addition which does use the extra beads in the upper and lower decks, but these beads are ultimately carried at the end of the process, so it is probably easier to skip those extra steps. The extra beads end up being far more useful for other operations, such as multiplication and division. What do we do?
We reset that wire, and move to the next wire. On the next wire, we run into the same problem. There are not enough beads on the wire to add one. So, again, we reset the wire and move to the next wire. Finally, we can register our single bead. The result looks like this:
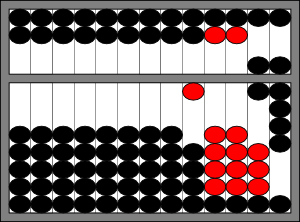
Finally, we finish the operation by adding 7 to the ones place.
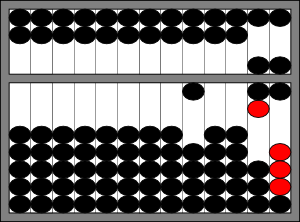
The result, 10,076, can be read from the abacus.
Subtraction works like addition, only in reverse. Beads are removed from the beam, and if there are not enough beads, one can be taken from the next wire to the left. One bead taken from the wire to the left has a value of 10, so we need to remember our addition facts to figure out how many beads we need to move to the beam. As the process is so similar, the details have been omitted from this post.
Other Operations
Of course, the power of the abacus does not end with addition and subtraction. There are several methods for multiplication and division, and there are ways to find roots. While the computations are relatively straightforward, they are a bit beyond the scope of this post. However, there are many resources out there for those that are interested.
There is a good discussion of multiplication at Abacus: Mystery of the Bead, and Paul Green’s book How to Use a Chinese Abacus: A Step-By-Step Guide to Addition, Subtraction, Multiplication, Division, Roots, and More provides very complete instructions on a number of operations. Other resources can be found in the footnotes, below.