About 2,500 years ago, mathematics was dominated by the Greek mathematician and philosopher Pythagoras. Pythagoras and his followers formed an almost religious group, complete with secret symbols, mysticism, and a dogmatic approach to mathematics. One of the important aspects of Pythagorean mathematics was the idea that, in essence, any distance could be measured with a kind of universal measuring stick.
To get an idea of what this means, we can consider figures on a plane. Specifically, suppose that we have a triangle, and we want to know the measures of its sides. We might start by declaring the height of the triangle to be equal to the length of our universal measuring stick.
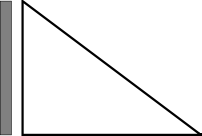
Now that we know the length of one side (i.e. we know that the height of the triangle is “one universal measuring stick”), we can try to measure the other sides. Unfortunately, as soon as we try to measure the width of the triangle, we run into a problem. One universal measuring stick is too short, but two universal measuring sticks are too long.
We might be tempted to give up, but a clever Pythagorean has the solution: put several triangles next to each other, and see if something works out. When we do this, it turns out that 3 triangles are exactly as long as 4 of our universal measuring sticks.
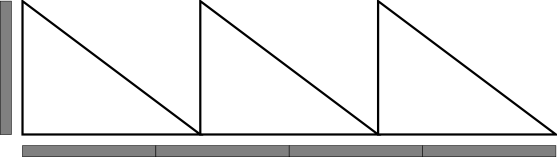
We could express this idea as a ratio. The ratio of the width of the triangle to height of the triangle is 4:3. That is, the width of the triangle can be found by gluing 4 universal measuring sticks together, then dividing the result into 3 equally sized pieces. This ratio, which expresses the width of the triangle as measured by our universal measuring stick, can also be expressed as the fraction \(\frac{4}{3}\).
The Pythagoreans believed that any two measurements could be related in the manner above. Given two different lengths, a Pythagorean would make copies and glue them together (metaphorically speaking) until both sets of measurements came out to a common length. In the example below, a Pythagorean would have made five copies of the blue length and three copies of the red length, whereupon both the blue and red sticks measure the same length.

It might take many hundreds or thousands of little blue and red lengths before the two sticks come out to the same length, but it was a fundamental belief of the Pythagoreans that, eventually, a common length could be found.
In essence, this means that the Pythagoreans believed that all numbers were rational. That is, all numbers could be expressed as a ratio of two natural numbers (where natural numbers are whole numbers, or counting numbers: the numbers \(1, 2, 3, \ldots\)). Note that the idea of rationality refers to the fact that rational numbers can be expressed as a ratio.
At this point, Pythagorean dogmatism enters into the picture. You see, it can be proved that there are numbers which cannot be expressed as ratios. As an example, consider another right triangle.
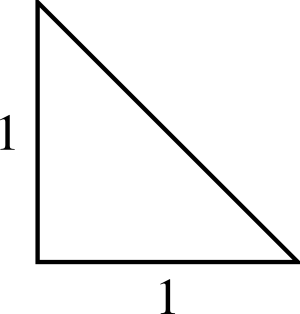
This right triangle has two legs which measure one unit in length (i.e. one foot, or one centimeter, or one furlong—the exact units don’t matter). According to the Pythagorean theorem, the hypotenuse of the triangle must measure \(\sqrt{1^2+1^2} = \sqrt{2}\) units in length. If the Pythagoreans are right, then it must be possible to express \(\sqrt{2}\) as a ratio.
The next several paragraphs feature a somewhat hairy mathematical argument. I encourage you to work through it, but if notation and logic scare you, skip to the material following the box.
For the time being, let’s assume that the Pythagoreans are right, and that there are two natural numbers \(m\) and \(n\) such that \(\sqrt{2} = \frac{m}{n}\). This is equivalent to saying that \(m\) legs of the triangle will be the same length as \(n\) hypotenuses.
Since \(\sqrt{2} = \frac{m}{n}\), we can square both sides, which implies that \(2 = \frac{m^2}{n^2}\). Applying just a bit more algebra, and multiplying both sides of this equation by \(n^2\), we have \(2n^2 = m^2\).
This next bit is a little tricky, so pay attention.
Any number can be expressed as the product of one or more prime numbers. For instance, 60 is equal to \(2^2\cdot 3\cdot 5\). When a number is squared, the power on each prime factor is doubled. So \(60^2 = 2^4\cdot 3^2\cdot 5^2\). Suppose that \(m\) is expressed in terms of its prime factors. It might look like this: \(m = 2^{q}\cdot 3^{q_1}\cdot 5^{q_2}\cdots\). In reality, we only care about the twos, so we can lump all of the other factors together, giving us \(m=2^{q}\cdot x\), where \(x\) is the product of all of the other factors. Similarly, \(n\) can be expressed as the product of its factors. Again, lumping together factors other than two, we have \(n=2^r\cdot y\).
Plugging these new expressions into the original equation, we have \(2\cdot (2^{2r}\cdot y^2) = 2^{2q}\cdot x^2\). Simplifying the left hand side of the equation, we get \((2^{2r+1}\cdot y^2) = 2^{2q}\cdot x^2\). Two numbers are equal if they have the same prime factorization, and they are not equal if they have different prime factorizations. Specifically, this means that \(2r+1\) and \(2q\) must be equal. Unfortunately, this is impossible. \(2r+1\) is an odd number, and \(2q\) is an even number, so the two numbers cannot be the same.
Clearly, we made a mistake somewhere, because we have concluded that an even number is equal to an odd number. However, the argument is sound all the way through, which means that the only place that we could have made a mistake is at the beginning, when we assumed that \(\sqrt{2}\) is a rational number, and can be expressed as the ratio of \(m\) and \(n\).
Therefore we are forced to conclude that the assumption is false, and that \(\sqrt{2}\) is not, in fact, a rational number.
To make a long story short, \(\sqrt{2}\) cannot be expressed as a ratio. Which means that you now know something very dangerous: according to the mythology of mathematics, the Greek mathematician Hippasus first demonstrated that \(\sqrt{2}\) is not rational while at sea. The Pythagoreans aboard the ship became so enraged by the heretical discovery that they threw Hippasus overboard to drown 1Weisstein, Eric W. “Irrational Number.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/IrrationalNumber.html..
