When students are first taught mathematics, the skills that they learn are concrete, and the teaching methodologies are equally concrete. When taught to add, students might physically group blocks, for instance by counting one group of blocks, then another, and finally combining the two groups and counting up the result. Subtraction is equally concrete: students might be given some blocks, then asked to remove a certain number, and count the remaining blocks.
Multiplication and division are also introduced in a concrete fashion. While many techniques are taught for both operations, they are both initially viewed as collecting several identical sets of objects, or dividing a large group of objects into smaller, equally sized groups. Once again, students might be given actual objects (blocks, candies, or tokens) to manipulate.
Then at some point in middle or high school, students are required to think in a radically different manner. Algebra is introduced, and students are asked to manipulate abstract variables, and to balance equations. This transition can often be quite difficult, especially when viewed in terms of cognitive development: many of the students introduced to algebra simply do not have the cognitive capacity to think abstractly.
Fortunately, there are things that instructors can do to help.
This week, I was introduced to one such technique by one of my teaching mentors, Pam Calhoun. She calls this trick “Bones.” The idea is that every formula has a skeleton, made up of several bones. Before putting any numbers into a formula, a student should write down the bones, giving themselves a scaffold or framework for finding the desired quantity.
For instance, consider the formula used for finding the slope of the line between two points. The points are given in tuple form (i.e. \((x,y)\)), and students are required to us the slope formula to find the slope. For example, let us find the slope of the line between the points \((5,2)\) and \((-3,6)\). First, we are going to have to remember the slope formula \({y_2-y_1\over x_2-x_1}\).
Next, we need to correctly identify the variables (never mind that the choice of \((x_1,y_1)\) is entirely arbitrary): \(x_1=5\), \(y_1=2\), \(x_2=-3\), and \(y_2=6\). Having identified each of the four variables, we now substitute the values into the formula, to get \({y_2-y_1\over x_2-x_1} = {2-6\over 5-(-3)}\).
Finally, we evaluate the expression and simplify to get a result: \({2-6\over 5-(-3)} = {2-6\over 5+3} = {4\over 8} = {1\over 2}\).
Having done all of this, we now know that the slope of the line is \(\frac{1}{2}\). This is a long process with many steps, several of which require some abstract thinking. For many students, the most difficult step is substituting numbers for variables. The idea that a letter can represent a number is, for some reason, incredibly hard for many students to understand.
So instead of presenting the formula above, with variables and all, we can present the following bones:
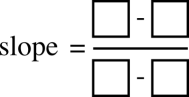
The above figure is the skeleton of the slope formula. This skeleton has several advantages over the standard \({y_2-y_1\over x_2-x_1}\). First and foremost, it removes one level of abstraction. To a 12 or 13 year old student (and there are many bright 12 and 13 year olds that take algebra), the boxes are clearly spaces that need to be filled with something. The boxes make it clear that they need to write something in. A variable is abstract; a blank box is concrete.
Also, this structure can help students keep track of signs and other notation that can often get lost. The x-coordinate from the second point is copied into the box directly, making it more difficult to lose the negative sign in front of the 3. In general, signs and other important notational decoration
The concept of bones is also fairly generalizable. For instance, once we find the slope, we might have another set of bones for the slope-intercept form of an equation:
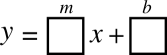
Notice that in this case, I have labeled the two boxes m and b. I could have done the same in the slope formula, above (either by labeling the boxes \(y_1\), \(y_2\), &c., or by giving the students the formula \(\frac{y}{x}\) as a model). This is another step which can help students move from the concrete to the abstract.
We could also replace the boxes above with either blank lines (e.g. ___ ) or an empty set of parentheses (e.g. \((\ \ )\) ). In fact, it is probably best that students eventually learn to use parentheses or brackets, as these are a common mathematical symbol, and should be easily understood by any future mathematics teachers or tutors that the students encounter. The important thing about bones is not the actual form of the blank spaces, but that the blank spaces are made obvious, and that they can be filled in by the students.
This week, I saw Pam using bones to teach seventh and eighth grade students to work with the two formulae above (the slope formula, and the slope-intercept form of a linear equation), and it amazed me how quickly they caught on to what was happening. She showed them the bones, gave them one example, and they were off to the races. Because they knew what the bones of an equation were, she did not have to teach them any variable manipulation or substitution. In fact, she did not even use the terms \(x_1\), \(x_2\), &c. until the end of the lesson!
In short, teaching students to see the skeleton or bones of a formula or equation is an excellent way of making the problem more concrete, and of separating out steps that may often be conflated. It reduces the chances of losing important pieces of notation, and gives students a highly generalizable method for working with unfamiliar problems.
Whenever students are attempting to work through a new type of problem, just show them the bones.
