Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say 1, and the host, who knows what’s behind the doors, opens another door, say 3, which has a goat. He says to you, “Do you want to pick door 2?” Is it to your advantage to switch your choice of doors?1http://www.marilynvossavant.com/articles/gameshow.html
This problem, called the Monty Hall Problem, is one of my favorite mathematical puzzles. Because it has been discussed to death (a quick Google search brings up hundreds of thousands of results), there is probably not much that I can add to the discussion. That being said, it is an interesting problem, and I think that it is worth sharing.
First, the solution: it turns out that you are better off switching. Consider the following decision tree:
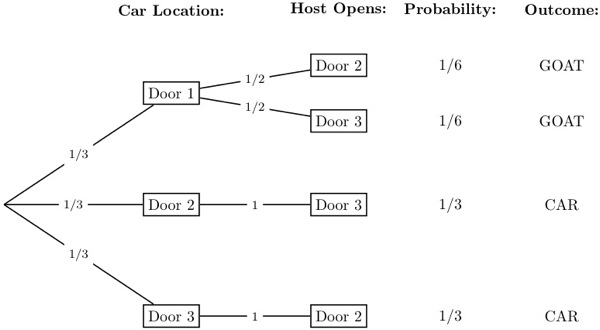
The tree assumes that we start by choosing door 1, and that we always switch. If the car was behind door 1, which will be the case 1/3 of the time, we will lose by switching. On the other hand, if the car is behind either door 2 or 3, which will be the case 2/3 of the time, then we win by switching. Nearly identical trees could be drawn for choosing door 2 or door 3 first, and our result would be the same.
What is interesting about this problem is that it plays with our sense of intuition. Most people assume that there is no advantage in switching. They reason that, because one door must hide a car and the other a goat, the odds of selecting the car by switching must be 50/50. Thus it doesn’t matter if we stay or switch—it would be equivalent to flipping a coin.
As demonstrated above, this reasoning is incorrect, but it is relatively convincing. In fact, when the problem was first published in Marilyn vos Savant’s Parade column, she received thousands of replies arguing that there was no advantage in switching. Still more surprising is the fact that many of these replies came from highly educated mathematicians and statisticians. Even highly trained mathematical minds have trouble arriving at the correct solution to this problem!
What is surprising is how simple the solution is to derive. There are many problems in mathematics that are far beyond abilities of mere mortals. They require years of training and work in highly specialized sub-fields, and the results are as incomprehensible as the questions themselves. The Monty Hall Problem is not one of these problems. In fact, many students in introductory level probability and statistics classes are given the tools necessary to properly formulate and describe the problem in the first couple of weeks of lecture or reading.
The problem is simply stated, easily understood, and not to difficult to solve, yet even intelligent people with a large amount of specialized and relevant knowledge are are tripped up by the Monty Hall Problem. It is this contrast that is interesting to me.
The Monty Hall Problem forces thinking individuals to examine their thinking process. It attacks common sense, and assaults intuition. As demonstrated by the responses to vos Savant’s column, the reactions to this were often angry and vicious. How is it that a simple mathematics puzzle can be so divisive and polarizing?
